あけましておめでとうございます。白ヤギの物理担当、シバタアキラ(@punkphysicist)です。

皆様はどんなお正月を過ごされましたか？日本の正月といえば、おせち、日本酒、おばあちゃん、そしてパズル、ですよね。私の正月はそんな感じでした。お節をたらふく食べ、美味しいお酒でほろ酔い気分になっている私の横で、黙々とおばあちゃんがパズルをやっているのに気づいたのです。部屋中をフワフワしている私とは全く対照的に、微動だにせずパズルを続けるおばあちゃん。御年迎えられると辛抱強さが半端ない。

そんなおばあちゃんがやっていたのはかわいいチョコレートのピースとは裏腹にこんな挑発的な文言の書かれたパズルです（この記事はアフィリエイトではありませんが、写真をクリックすると買えます）

何時間たっても答えが出ないおばあちゃん、辛抱強さは人一倍強いですが、私も何とか助けてあげたいと思いトライ。しかし日本酒が・・・と言うのは言い訳でめっぽうパズルに弱い。しかしそこは元物理学者の意地を見せなくてはなりませぬ。早速MacBook Airを取り出し、ガシガシとコードを書き始めました。

class Board(object):
    def __init__(self, shape=[6,10]):
        self.v=np.zeros(shape)
    def __iadd__(self, p):
        loc=p.loc
        shape=p.shape
        self.v[loc[0]:loc[0]+shape[0], loc[1]:loc[1]+shape[1]]+=p.rotated
        return self
    def find_loc(self):
        return (random.choice(range(self.v.shape[0])), random.choice(range(self.v.shape[1])))
    def test1(self):
        for i in range(self.v.shape[0]):
            for j in range(self.v.shape[1]):
                if self.v[i,j]!=1: return False
        return True

まずはボードを定義。6×10のマスの中にチョコレートを入れるためにランダムなロケーションを呼び出せるようにし、最終的にボード全体が埋まる（1になる）と、終了、ということです。

class Piece(object):
    def __init__(self, array, loc=[0,0], rot=0, flip=False):
        self.v=np.array(array)
        self.loc=loc
        self.rot=rot
        self.flip=flip
    @property
    def shape(self): return self.rotated.shape
    @property
    def rotated(self):
        if not self.flip:
            return np.rot90(self.v, self.rot)
        else:
            return np.fliplr(np.rot90(self.v, self.rot))

一方チョコレートのピースは、回転したりひっくり返したりで、場所に加えて8パターンの置き方が有ります。このへんはNumpyがいい感じにやってくれます。ここからはちょっとハショりますが、各ピースを定義：

def get_pieces():
  ps=[]
  ps.append(Piece([[0,1,0],
                   [1,1,1],
                   [0,1,0]]))
  ps.append(Piece([[0,1,0],
                   [0,1,0],
                   [1,1,1]]))
  ps.append(Piece([[0,1,0],
                   [1,1,1],
                   [0,0,1]]))
...

何を隠そう私はモンテカルロ法ばっかり使ってきましたので、サイコロを転がすのが大好きです。日本酒を飲みながらガンガンランダム関数を呼び出します。「パパすごい！それで解けちゃうの？」そんな言葉に自尊心をくすぐられます。

def try_one(b,p):
    p.loc=b.find_loc()
    p.rot=random.choice(range(4))
    p.flip=random.choice([True,False])
    try:
        b+=p
        return True
    #端においた時にエラーになる
    except ValueError:
        return False

後はこれを答えが出るまで呼び続ければおばあちゃんの代わりにパイソン君がやってくれる。さすがっ

def main():
    count=0
    while 1:
      board=Board([6,10])
      nogood=False
      for p in ps:
          # 一個ピースを置いてみる
          while try_one(board, p)==False:
              pass
      count+=1
      if count%1000==0:
          print count
      # 答えが出たら終了！
      if board.test1():
          print_ps(ps)
          break

というところまで書いて、勇み足でwhileループを回し始めました

if __name__=='__main__':
    main(1)

おばあちゃんが一時間かかって数通りしかできないところをパイソン使えば何万回でもできるぜ、とニコニコしながらアウトプットを眺めます。

77000
78000
79000
80000
81000
82000
83000
84000
85000
86000
87000
88000...

しかし、whileループを数百万回回したところで気分が空回りし始めます。
「果たして解は見つかるのだろうか・・・・」
「いや、回し続ければかならず見つかるはず・・・・」
「次の瞬間かも、止めない方がいい・・・」

「それにしても時間がかかるな・・・」
「あの8コア乗ったEC2、未だ起きてたはず。正月だし、いいだろ・・・・」
「screen使えばいくつでも同時に走らせられるぜ・・・・」
「おぉhtopでみるとコア全部回ってる、快感」
「待ってるのも暇だからWiiでもやろ・・・」

そして翌朝、ウキウキしながら開いてみると、数億回回って回り続けてるプロセスが8つ。異変に気づきます。家族もだんだん「休みくらいパソコンやめたら」モードに。よって日本酒。

そしてふと、「何通りくらい置き方あるんだろ」とおもった

60個のマスに12個のピースを置く方法を計算してみると・・・確か60C12

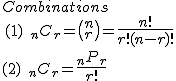
60C12=1,399,358,844,975

1兆超えてた。

プログラムが早ければ1兆でも回せばいいのでしょうが、ランダム関数が多用されててそれもままならない様子。ちょっとマジメな話をすると、非常に少数の回を探すような問題の時は、モンテカルロ法は全然適してないです。一回一回が計算しようとしている答えに貢献するような計算（例えば積分とか）そういう時には数学的な解法よりも時間的な優位性が有ります。

そろそろすけっとが必要です。恥など気にしている場合ではありません。おばあちゃんを救わなくては。
思い出したのは、今年のPyConJPで線形計画問題を解決するライブラリ、pulpを使って、あらゆるパズルを解くというすごいプレゼンをされた、構造計画研究所の斉藤さんです:

数独なんかも20行位のコードで解いてしまう、そして次から次にあらゆるパズルを解いてしまうプレゼンは圧巻です。

斉藤様

あけましておめでとうございます。
昨年PyCon JPにて少し質問させていただきました、白ヤギコーポレーションのシバタと申します。

年始早々恐縮でありますが、ひとつご相談がありご連絡いたしました。
と言いますのも、正月のレクリエーションとして、添付の写真のようなパズルを
かれこれ2日ほどやっているわけでありますが、なかなか解けず、
とうとうプログラムでとくことにしたのですが、いつまでたっても計算終了しません。
現行かなりシンプルなプログラムで、各ピースをどのポジションに置くのか、
（プラス、回転とフリップが有ります）をランダムに決定し試しているだけなのですが、
6x10=60のポジションの中から11ピースの置き場を決める組み合わせは1兆通り以上
あるということがわかり、いくら計算しても解が出ない状況です。
現行のプログラムを添付しました。
（ピース数を制限した場合は解を見つけることが出来ました）

PyConでお話されていたPulpはこのような問題解決には使えるでしょうか？
斉藤さんの例を見せていただいたのですが、こういった事例がなく、もしかしたら
適さないのかな、という印象です。いずれにしても、このパズルの解を探すのにあたり、
もし何かいい案があれば教えて頂けないでしょうか？

ただの遊びですので、お忙しければ無視してください。
されど遊び、もしなにかご名案があればご参加いただけましたら幸いです。

何卒よろしくお願い致します。

白ヤギコーポレーション
シバタ

「恐縮」と言いながら人の正月の邪魔をするただの迷惑なやつです。こんなならず者に返事などもらえるはずないと諦めていたところ、

シバタ様
構造計画の斉藤です。
メールありがとうございます。

あけましておめでとうございます。

ペントミノパズルは、数理計画でも解けます(下記参考)が、
サイズが大きいと、厳しいです。
http://www21.tok2.com/home/kainaga11/glpkPent/glpkPent.htm

参考までに、バックトラックで調べるものを添付します。

また、よろしくお願いします。
—
(株)構造計画研究所 事業開発部 斉藤 努

天使現る。

で「バックトラック」って何かというと京都産業大の先生によると

バックトラック法 (backtracking）あるいは後戻り法とは，問題の解を見つけるために， 解の候補をすべて調べることを組織的にかつ効率よく行うための技法である。 難しい組み合わせ的な問題を解くための技法であり，応用範囲も広い。 　数多くの組み合わせの中から，ある条件を満たすものを見つけたり， 評価値のもっとも良いものを見つけたりする問題を考えよう。 問題の構造を解析して，方程式を解くような解法があればよいが， そうではなく， 解の候補になりうるものを片端から調べ上げる以外に手がない場合がある。 このようなときに，役に立つなアルゴリズムがバックトラック法である。 　ほとんどの組み合わせ的な問題においては，解をもとめるための方程式は存在せず， バックトラック法が唯一の解法であることが多い。

まさに明治のチョコレート問題がこれであります。バックトラック法を使うとどうして早いかというと、解が存在しない組み合わを含む候補は、それがわかった時点でかたまりごと切り捨てることができるという点です。例えば、左上にピース1をおき、その真横にピース3をおいたら、2つのピースがかぶってしまう、なんていう場合、この2つのピースの置き方を含む組み合わせはそれ以降一切考えなくていいわけです。当然といえば当然ですが、日本酒は時としてそういった考え方の妨げになってしまうことが有ります。このようにして、ダメなルートが見つかったらそこをどんどん塞いでいき、必要最小限のトライで解を見つける方法なのです。モンテカルロ馬鹿な物理学崩れは、酔いが冷めてもこんなことはできないわけです。

斉藤さんのエレガントな解答をみてみましょう。

import numpy as np
class Piece:
    def __init__(self, s, t):
        h = t // 100 # 縦
        m = (t // 10) % 10 # 反転する(2)/しない(1)
        n = t % 10 # 回転数
        a = np.array().reshape(h, -1)
        self.pos = -1
        self.sel = 0
        self.cand = []
        for i in range(m):
            for j in range(n):
                self.cand.append((a, a.argmax()))
                a = np.rot90(a)
            a = np.fliplr(a)
pp = [Piece('010111010', 311),
      Piece('111101', 214),
      Piece('110011001', 314),
      Piece('110011010', 324),
      Piece('110010011', 322),
      Piece('111110', 224),
      Piece('11100011', 224),
      Piece('11110100', 224),
      Piece('111010010', 314),
      Piece('11111000', 224),
      Piece('111100100', 314),
      Piece('11111', 112)]
def allp(pp):
    for i, p in enumerate(pp):
        if p.pos < 0:
            for j, c in enumerate(p.cand):
                yield i, j, c[0], c[1]

ここまでで、ピースを定義しています。回転しても意味のないものは事前に指定したり、無駄がありません。allpで、すべてのピースの置き方を事前に展開しています。毎回ランダム関数を呼ぶような、アホなことはしません。そしてここからがミソです

board = np.array([False] * 60).reshape(6, 10)
def chk(board, pp, x, y, lvl):
    for i, j, p, d in allp(pp):
        h, w = p.shape
        # ピースが飛び出したらそこから先は見ない
        if x - d < 0 or x - d + w > 10 or y + h > 6: continue
        b = board[y:y + h, x - d:x - d + w]
        # ピースがかぶったらそこから先は見ない
        if (b & p).any(): continue
        pp[i].sel = j
        pp[i].pos = y * 10 + x - d
        # すべてのピースを置ききったらTrueを返す（recursiveコールの終了）
        if lvl == 11: return True
        b += p
        k = board.argmin()
        # ここまで成功したら次のピースを試す
        if chk(board, pp, k % 10, k // 10, lvl + 1): return True
        # 失敗したら巻き戻して別の手を試す
        b -= p
        pp[i].pos = -1
    return False
chk(board, pp, 0, 0, 0)
l = np.zeros((6, 10))
for i, p in enumerate(pp):
    x, y, z = p.pos % 10, p.pos // 10, p.cand[p.sel][0]
    l[y:y + z.shape[0], x:x + z.shape[1]] += z * i
print('\n'.join(''.join(chr(int(j) + 65) for j in i) for i in l))

全体の行数にして私のコードの半分。記号のようなパイソンコードで、シャープな数学者の匂いがします。最後の行とかも、数字をアルファベットに変換しちゃううところなんかがニクイです。（もちろん途中のコメントは私が入れたものです。）これを走らせると、ものの3秒くらいでこのような結果が出ます。

BBBCCDDIII
BGBACCDDIL
GGAAACDJIL
GEEAJJJJKL
GEFFHHHHKL
EEFFFHKKKL

まさに知性の勝利です。まだまだCPUが人間の脳を置き換える時代は程遠いということがわかりました。

ちなみに頂いたリンクによると、このパズルの解は2000通りあるそうです。ここではそのうちの一つの解を示していただきましたが、リンク先のキューブ王はすごいです。パズル好きな方は是非一度ご覧になってみてください。マニアとはまさにこういう人のことですね。一体誰なんでしょうか。知っている方がいらっしゃったら情報求む。

お節に始まり、パズルまで。おかげさまで正月らしいことを全部出来た2015年の年始でした。斉藤さんどうもありがとうございました！
昨年は弊社のアプリ、カメリオもiTunesのベストアプリに選ばれ、いい年でしたが、今年もいい年になりそうです。

あと、弊社ではただいま絶賛エンジニア募集中ですので、興味のある方はこちらをご覧下さい。